 (Für die wichtigsten Unterschiede zwischen Supervised und Unsupervised Learning siehe auch den Beitrag).
(Für die wichtigsten Unterschiede zwischen Supervised und Unsupervised Learning siehe auch den Beitrag).
Was ist Unsupervised Learning?
Unsupervised Learning oder auch unüberwachtes Lernen versucht in den unbeschrifteten Daten Muster zu erkennen und/oder aus den Daten so viele Informationen wie möglich zu extrahieren. Unsupervised Learning:- arbeitet mit unbeschrifteten Daten
- hat keine Y (abhängige)-Variable zum Schätzen (üblich bei Supervised Learning Methoden wie Regression)
Wie funktioniert es in der Praxis?
Es gibt vom Prinzip zwei wichtige Aufgaben von UL Algorithmen. Sie können beispielsweise unstrukturierte Daten nach Ähnlichkeiten sortieren (Clustering Algorithmen). Dies wird u.a. im Marketing dazu genutzt, um große Kundendatenbestände nach ihren Merkmalen zu sortieren. Mit Clustering Algorithmen lässt sich gezielte Werbung leichter gestalten. Die Firmen können in ihren Werbekampagnen speziell auf die Merkmale spezifischer Kundengruppen eingehen. Eine weitere Sparte der UL-Algorithmen kann uns dabei helfen die Dimensionen eines großen Datensatzes (Big Data) zu reduzieren. Große Datensätze haben oft Hunderte von Features/Variablen. Das Arbeiten mit solchen Datensätzen gestaltet sich sehr schwierig und ist auch teuer. Hier kommen die sogenannten Dimensionality Reduction Algorithmen ins Spiel. Sie reduzieren die Anzahl an Features in einem Datensatz von zum Beispiel 100 Features auf 30 Features. Damit ist eine weitere Analyse, die Beschriftung der Daten und die Anwendung von Supervised Learning Algorithmen leichter. Insgesamt kann die Anwednung der Unsupervised Learning Algorithmen Kosten sparen, denn sie- reduziert die Menge an zubeschrifteten Daten,
- reduziert die Rechenzeit,
- ermöglicht gezieltes Aussuchen der Zielgruppen.
Die wichtigsten Unsupervised Learning Methoden
Clustering Algorithmen
Clusterting Algorithmen sortieren Daten nach Ähnlichkeit in Gruppen bzw. Cluster. In einem Cluster befinden sich Datenpunkte, die einander ähnlich sind.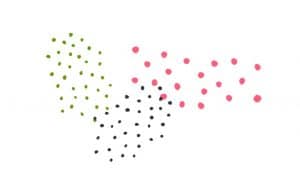
K-Means Algorithmus
K-Means gehört zu den populärsten Clustering Algorithmen. Vom Prinzip ordnet K-Means Datenpunkte, die nach bestimmten Kriterien als ähnlich klassifiziert werden in sogenannte Cluster.Cluster = Ansammlung an Datenpunkten, die nach Ähnlichkeit gruppiert sind
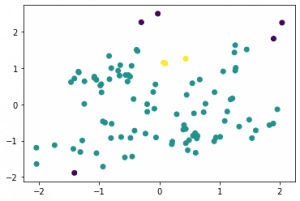
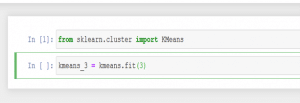 Auf Github habe ich weitere Beispiele für die K-Means Klassifizierung und Umsetzung in scikit-learn (anhand einer per Zufall generierten Distribution) veröffentlicht. Hier ein Beispielergebnis:
Auf Github habe ich weitere Beispiele für die K-Means Klassifizierung und Umsetzung in scikit-learn (anhand einer per Zufall generierten Distribution) veröffentlicht. Hier ein Beispielergebnis:

K-Means
Elbow Method
Die Verteilung oben könnte darauf hindeuten, dass im Datensatz zwei Cluster vorhanden sind. In der Praxis ist es nicht einfach die Anzahl der Cluster zu bestimmen. Wenn wir auch keine genaueren Kenntnisse und Vorstellungen über unseren Datensatz haben, kann uns bei der Clusterschätzung eine Berechnung, die sogenannte Elbow Method helfen. Zusammengefasst schätzt die Elbow Method die optimale Anzahl an Clustermenge (K). Die Optimale Anzahl sieht man auf der Visualisierung als eine Art Ellbogen (deshalb auch Elbow Method). Die Idee dahinter ist eine Art von „law of diminishing results“: ab einem bestimmten Punkt schwächt die zunehmende Anzahl an Cluster den Erkentnissgewinn aus dem Datensatz. Mathematisch wird im Rahmen der Ellbow Method die Varianz als WCSS (Within-Cluster Sum of Squares) für jeden K-Wert erfasst und auf einem Diagramm visuell dargestellt. Die Stelle, an der die Linie einen deutlichen Knick macht, gibt die optimale Anzahl an Clustern.
Ellbogen = optimale Anzahl an Clustern
In der Praxis ist der Ellbogen oft leider nicht so deutich zu erkennen. In der Regel müssen mehrer Herangehensweisen ausprobiert werden, um die optimale Anzahl an Clustern zu bestimmen. Vor der Anwendung von K-Means müssen die Features skaliert werden (Stichwort: Feature Skaling). K-Means Vorteile:- einfach in der Umsetzung
- schwer optimale Anzahl an Cluster zu bestimmen
- wenn die Clusterzentren nah beieinander liegen, funktioniert K-Means nicht zuverlässig
DBSCAN
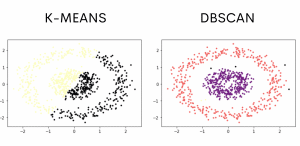
DBSCAN ist auch ein Clustering Algorithmus. Im Gegensatz zu K-Means ist bei seiner Anwendung die Bestimmung der Clusteranzahl nicht notwendig. In Fällen, wo die Clustermenge nicht einfach geschätzt werden kann, ist DBSCAN eine gute Alternative. DBSCAN steht für Density Based Spacial Clustering und ist, wie der Name bereits sagt, ein sogenannter „density-based“ Algorythmus, d.h. die Cluster werden hier anhand der Dichte der Datenpunkte bestimmt:„Density-Based Clustering refers to unsupervised learning methods that identify distinctive groups/clusters in the data, based on the idea that a cluster in data space is a contiguous region of high point density, separated from other such clusters by contiguous regions of low point density.“DBSCAN bestimmt Cluster basierend auf der Anzahl der Datenpunkte in der Umgebung: ein Datenpunkt wird ausgewählt, DBSCAN prüft, ob sich in seiner direkten Nachbarschaft eine bestimmte Anzahl weiterer Datenpunkte befindet. Wenn ja, dann wird diese Datenpunktmenge zu einem Cluster erklärt. Im Gegensatz zum K-Means versucht DBSCAN nicht alle Punkte einem Cluster zuzuordnen. Outlier sind möglich. Vom Prinzip ermöglicht es präzisere Ergebnisse. Der Nachteil ist aber, dass DBSCAN im Gegensatz zu K-Means oft mehr Cluster findet als im Datensatz vorhanden sind. Zum Vergleich habe ich DBSCAN auf den selben Datensatz aus dem oberen Beispiel(K-Means) angewandt:Nagesh Singh Chauhan (KD Nuggets)
DBSCAN
 DBSCAN Vorteile:
DBSCAN Vorteile:
- keine vordefinierte Clusteranzahl
- guter Umgang mit Outliers (nicht alle Datenpunkte werden als Cluster identifiziert)
- wenn die Dichte der Cluster variiert, hat DBSCAN Probleme die Cluster zu identifizieren
 Auch dieses Beispiel findet sich auf meinem GitHub Account.
Auch dieses Beispiel findet sich auf meinem GitHub Account.
Dimensionality Reduction Algorithmen
Die Dimensionality Reduction Algorithmen dienen in der Regel dazu die Daten vor der Anwendung der Supervised Learning Algorithmen zu transformieren. Einer der wichtsten Algoritmen in diesem Bereich ist die Principal Component Analysis oder auf Deutsch Hauptkomponentenanalyse.Principal Component Analysis (PCA) – Hauptkomponentenanalyse
PCA reduziert unsere Daten so, dass nur die wichtigsten Informationen im Datensatz erhalten bleiben. Mit Hilfe von PCA können wir die Anzahl der Variablen in unserem Datensatz reduzieren, dabei aber die wichtigsten Informationen aus dem Ursprungsdatensatz erhalten. Das PCA Verfahren ist insbesondere im Fall von Big Data hilfreich. In disem Fall beinhaltet ein Datensatz oft mehrere Hundert an Variablen, die man mit den Standradmethoden nur schwer bearbeiten und analysieren kann. Die Beschriftung von so einem großen Datensatz kann auch sehr teuer werden. Funktionsweise PCA funktioniert mit Hilfe sogenannter Feature Extraction:„it combines our input variables in a specific way, then we can drop the “least important” variables while still retaining the most valuable parts of all of the variables.“ Matt Brems „A One-Stop Shop for Principal Component Analysis„PCA reduziert die Anzahl der Featuers bzw. Variablen in unserem Datensatz. Aus einem Datensatz von beispielsweise 100 Features macht das PCA Verfahren einen Datensatz von 50 Features. Die Reduktion geschieht aber nicht durch das reine Entfernen von Variablen (sog Feature Elimination). Vielmehr werden die neuen Variablen aus den bereits bestehenden extrahiert (sog Feature Extraction) und in neue Variablen mittels mathematischen Berechnungen (Ähnlichkeiten) zusammengefasst. Ab Ende haben wir dadurch weniger Variablen. Visuell können wir uns die Hauptkomponentenanalyse wie folgt vorstellen:
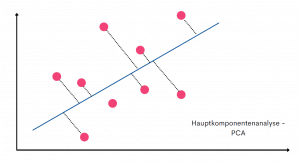
Principal Component Analysis
PCA in Scikit-Learn
- gute Bearbeitung von Datensätzen mit sehr vielen Variablen
- einfach in der Anwendung
- die Ergebnisse sind nicht leicht interpretierbar. Die neu erschaffenen Variablen sind nicht unbedigt verständlich
Unüberwachtes Lernen – Anwendung in der Praxis
In der Praxis werden die Unsupervised Learning Algorithmen sehr vielfältig eingesetzt. Eine der häufigsten Anwendung ist das Marketing. Viele Firmen haben große Kundendatensätze, die mit Hilfe von PCA auf die wenigen Features reduziert werden können. Auch Clustering wird angewandt, um Kunden nach ihren Merkmalen zu sortieren und auf diese Weise gezieltere Werbung zu gestalten. Generell ist die Reduktion der Features in einem Datesatz aus Kostengründen nützlich. Einen Big Data Datensatz zu beschriften kann recht schnell teuer werden. Ein weiteres Feld ist Medizindiagnostik:„Automatically generated information from unstructured data could be exceptionally useful not only in order to gain insight into quality, safety, and performance, but also for early diagnosis.“ Sidey-Gibbons in „Machine learning in medicine: a practical introduction„Hier werden die Unsupervised Learning Methoden auch sehr vielseitig eingesetzt, u.a. im Bereich Diagnostik, Anomalie-Erkennung und MR-Scans. https://datenverstehen.de/ml-algorithmen-unsupervised-supervised-learning







Hi Alex, endlich habe ich Zeit gefunden mir das Account anzuschauen und tatsächlich gibt es auf dem Account einige Unregelmäßigkeiten.…
Hallo, ich werde mir das Profil angucken und poste hier, was ich gefunden habe. Ich brauche aber noch ca. Eine…
Hi Aleksandra, ich glaube, mit deiner Analyse könntest du vielen Menschen helfen, die betrogen werden. Insbesondere in der Krypta-Welt. Dort…
Größerer und allumfassender Algorithmus: Die Schwerkraft ist keine Kraft, die von A nach B reicht, sondern ein grundlegendes und elementares…
Hallo, ja. es geht um dieses Projekt (optiizedSD=Projekt von Basu Jindal)