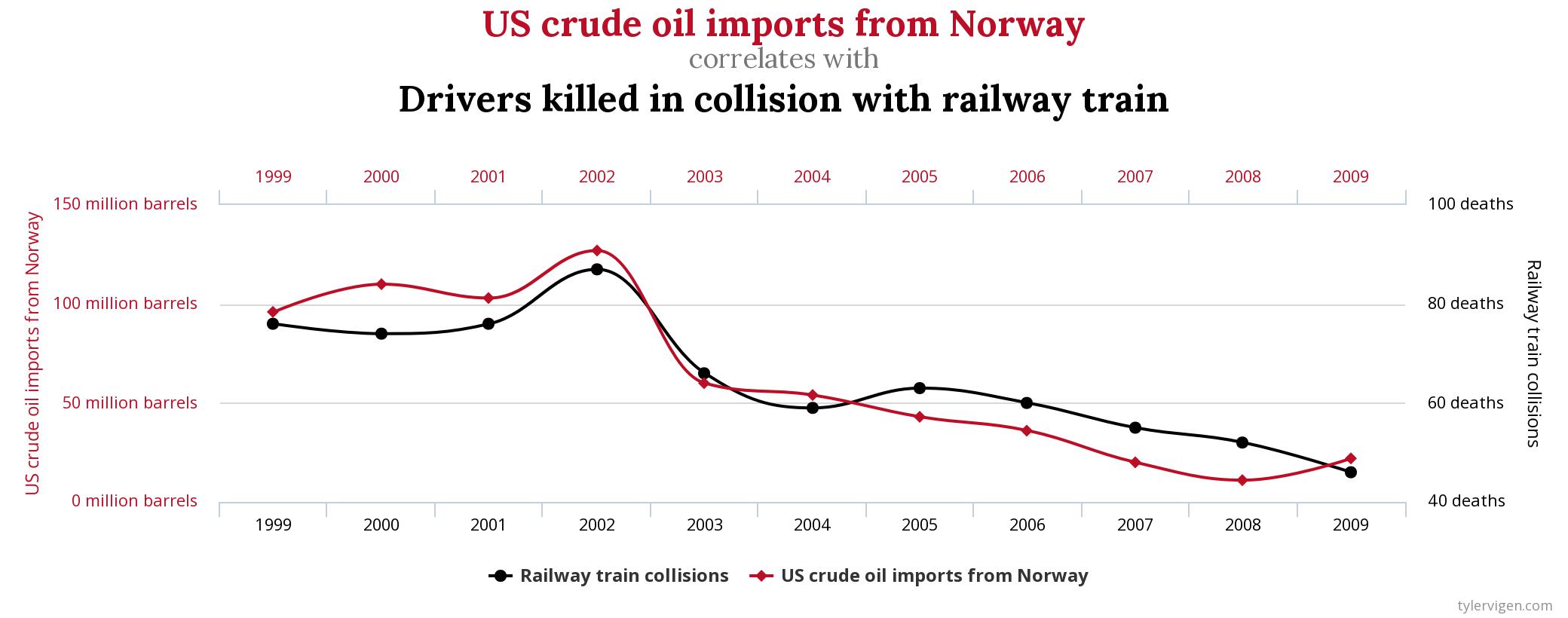
Die obige Statistik zeigt, dass offenbar die Zahl der Fahrer, die in einr Kollision mit einem Zug ums Leben gekommen sind, mit der Zahl der Ölimporte aus Norwegen stark korreliert. Zumindest in den USA…

Diese Statistik bringt uns zu einem interessanten, aber auch ernsten Konzept – und zwar der Idee der Scheinkorrelation (spurious correlation auf Englisch).

Inhalte Verbergen
1 Definition
2 Das Problem – Korrelation
3 Scheinkorrelation in Big Data

Definition

Vom Prinzip geht es darum, dass völlig unabhängige Phänomene wie zum Beispiel die monatliche Durchschnittstemperatur in Ulan-Bator (Mongolei) und der DAX Index 1 zu 1 miteinander vergleichbar sein könnten, d.h. sich fast deckungsgleich bewegen. Dies könnte ja bedeuten, dass es dort einen kausalen Zusammenhang gibt, d.h. wenn die Temperatur in Ulan-Bator steigt, steigt auch der Dax usw.

Das ist das Prinzip der Scheinkorrelation, welches eindrucksvoll von Tyler Vigen auf seinem Blog Spurious Correlations belegt wird. Vigen stellt Werte zusammen, die eigentlich keine sinnvolle Verbindung miteinander haben können, wie in diesem Chart unten. Die Zahl, der Leute, die im Schwimmbad ertrunken sind und die Zahl der Filme, in denen Nicholas Cage im gegebenen Jahr aufgetreten ist:

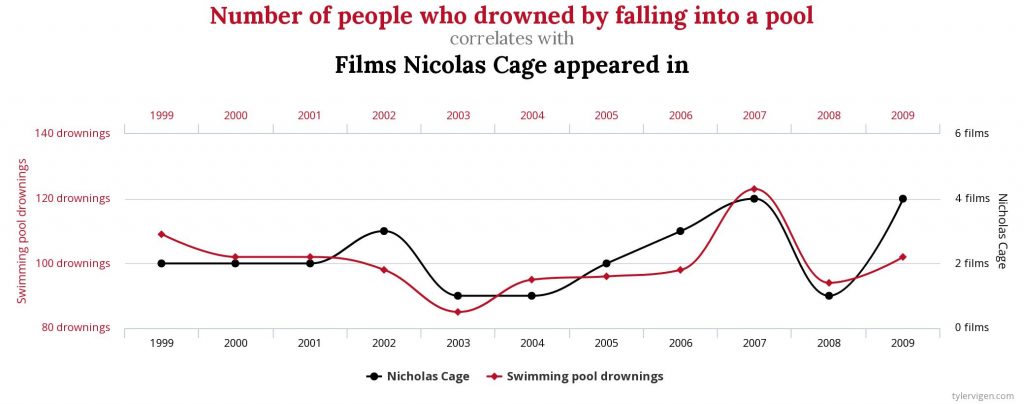
Scheinkorrelation (Quelle: Tyler Vigen)

Die obere Grafik zeigt eigentlich, dass der Schein nicht trügt. Offenbar hängt die Zahl der Filme von Nicholas Cage mit der Zahl der im Schwimmbad Ertrunkenen tatsächlich zusammen.

Oder auch nicht…

Das Problem – Korrelation

Offensichtlich zeigen die oberen Grafiken Scheinkorrelationen. Sie gaukeln einem einen kausalen Zusammenhang oder einfach nur eine Korrelation vor, obwohl die zwei Variablen nichts mit einander zu tun haben.

Korrelation bedeutet, dass sich mehrere Werte/Variablen miteinander bewegen. So wie eben auf diesen Bildern.

Negeative Korrelation bedeutet: je mehr ein Wert A zunimmt, desto mehr nimmt der Wert B ab. Zum Beispiel: Je mehr ich die Unternehmensbesteuerung erhöhe, desto weniger Unternehmen werden gegründet.

Positive Korrelation dagegen bedeutet, dass beide Werte gelichzeitig zunehmen:

Manche Werte können miteinander sinnvoll korrelieren. Wenn ich auf der Straße viele Menschen mit Regenschirmen sehe, dann weiß ich, es könnte heute regnen. Es ist eine Korrelation, denn es regnet ja nicht, weil die Leute Regenschirme tragen.

Scheinkorrelation in Big Data

Scheinkorrelation ist insbesondere in großen Datenmengen vertreten, sogenannten „Big Data“. Aufgrund der schieren Größe beinhalten sie viele Variablen. In so einer Umgebung ist der Weg eine Scheinkorrelation zu finden und dann sie auch noch kausal zu begründen nicht schwer.

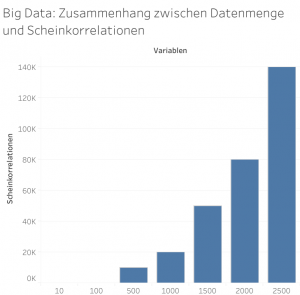
Aufgrund der Größe der Datensätze kann sich dann der Forscher/Data Scientist eben bestimmte Zusammenhänge herauspicken und sie auch kausal begründen, obwohl es sich nur um Scheinkorrelationen handelt.

Es ist wichtig festzuhalten: je größer die Datenmenge, desto größer die Gefahr von Scheinkorrelationen.

„This is the tragedy of big data: The more variables, the more correlations that can show significance. Falsity also grows faster than information; it is nonlinear (convex) with respect to data (this convexity in fact resembles that of a financial option payoff). Noise is antifragile.“

Nassim Taleb für Wired

Man kann sich die Big Data als ein Rauschen vorstellen, aus dem wir eben ein Signal hören möchten. Eine sinnvolle Information mit Bedeutung. Leider ist es schwierig das Signal richtig herauszuarbeiten. Wenn es das gesuchte Signal überhaupt gibt. Dazu kommt noch der Anreiz für den Forscher einen Zusammenhang oder Korrelation zu finden. Niemand hört gerne, dass das Rauschen eben kein Signal überdeckt.